多辊辊弯成形工艺设计方法的对比研究
摘要:以某U型槽钢的辊弯成形为例,比较了经验公式、专业软件COPRA和数值模拟进行辊弯成形工艺设计的特点。发现现有经验公式均有一定的适用范围,一些公式求解结果的误差很大;利用COPRA软件可以得到对实践具有参考价值的结果,结合经验公式可提高分析效率。数值模拟功能强大,信息完整,但操作的要求较高,且分析计算效率较低。
关键词:辊弯成形;工艺分析;COPRA;数值模拟
辊弯成形是通过顺序配置的多道次具有特定轮廓型面的成形轧辊,把金属卷材或单张板材逐渐地进行横向弯曲,以制成特定断面的长条型材。辊弯变形复杂,成形质量受轧辊速度、成形道次数、道次间距、成形弯曲角等众多因素的影响。这方面已进行许多研究,如QVBui[1]等分析模拟了辊弯成形过程,把纵向压力和位移轨迹的模拟结果与实验结果进行对比,发现屈服极限和加工硬化对质量影响很大。Bhattacharyya,Smith[2-3]研究了单辊和多辊情况变的变化。郑军兴等[4-5]研究了板厚、成形道次对冷弯成形过程及回弹的影响;付磊分析了轧辊间距对冷弯成形的影响。
辊弯变形复杂,辊弯成形规律尚未被完全掌握和认识。目前辊弯型钢的工艺设计多以经验设计为主,有必要进一步探索高效、准确的设计途径。本文以某U型槽钢的辊弯成形为例,比较了采用经验公式、专业设计软件COPRA以及数值模拟进行冷弯成形工艺设计的特点。
1 辊弯成形U型钢参数
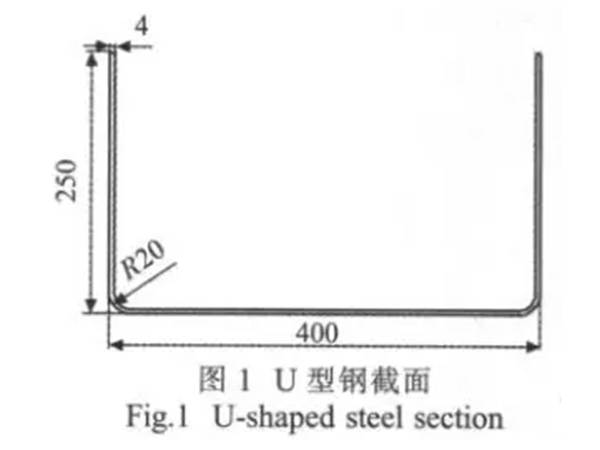
U型钢如图1所示,材料采用屈服强度为418MPa的高强度钢,板厚为4mm,弯曲角度90°。
2 经验公式分析
2.1道次数
小奈弘[7]根据实际生产所用的各种断面型材与成形道次数,整理出了对称断面、非对称断面、宽幅断面和圆管的成形因子Φ与成形道次N的关系。定义对称断面的成形因子Φ是断面总弯曲角数n、板厚t及左右立边长度和F之积。由于底部腹板只送断面型材,不参与弯曲,故形状因子不包括腹板宽度。
根据图1所示的断面形状与尺寸,全立边长度F=2×250mm,全弯曲角数n=2,板厚t=4mm则形状因子函数:
Φ=Fnt=4000
将形状因子函数与文献[7]中图2对比,Φ值大于图中最大值,所以不宜采用。
治·哈姆斯[8]提出了如下的道次计算经验公式:
式中:N为道次数;h为最大截面高度;t为材料厚度;θ为成形基准一侧成形的总角度数;Y为屈服应力;U为抗拉强度;z为预冲孔和板料连接系数;s为形状系数;e为额外增加道次数;f为公差系数。将图1参数(其中h=250mm,t=4mm,θ=1°,z=0,s=1,e=0,f=0)代入式(1),得N=130.139。显然该数值过大。
赵艳红利用成形角法给出确定成形道次数N的基本方法[9]:
N=(H/L)cotθ (2)
式中:弯曲高度H=250mm,机架间距L=1300mm,成形角θ=1.5°,可得N=7.34。取N=8,该道次数比较符合实际情况。
可见,以上经验公式均有一定的适用范围,一些公式的道次数求解结果误差很大。
2.2弯曲角分配
各道次弯曲角的分配由板厚、道次间距、机架间距、变形速度、总变形量等因素决定。成形初期取较小的弯曲角以避免强迫咬入,中期则应避免由于弯曲角分配不均而造成带坯局部异常变形以及表面划伤,后期采用较小变形量以防止回弹。可采用余弦曲线来分配弯曲角[9]:
式中:N为道次数;θs为单边总弯曲角度;θi为第i道次的弯曲角。由此,可求出图1制件成形弯曲角的分配方案(表1)。
2.3过弯角度的计算
为了防止切口变形,在最终道次前设置过弯轧辊,可采用过弯角度实验公式[7]:

式中:θopt为最终弯曲角;H为边腿高度;t为板料厚度。
3 COPRA工艺优化
COPRA是冷弯成形设计软件系统,需要与Au—toCAD配合使用。COPRA提供了定半径法,定中线长度法,轨迹法,角度/半径法四种不同的弯曲展开方法。展开方法取决于需成形的断面,常用的是定中性线法或定半径法。每个弯曲实体每个弯曲实体都由内半径、弯曲角以及中性线长度来描述。本例中材料为高强度钢,成形回弹较大,采用定半径法可以减小回弹。输入相应参数到COPRA,模拟结果如图2。可以看出,大部分道次的应变接近于2%,需要适当降低。图3为优化后的模拟结果,各道次弯曲角如表2。可以看出,各个道次的应变均小于0.6%,应变效果比较理想。选择BISWAS过弯的方法对最后道次计算回弹,得到最终弯曲角度为100.38°,与经验公式计算结果吻合。
4 数值模拟
4.1模拟方案

多道次辊弯成形有限元模型规模大,边界条件复杂,是一个高度非线性准静态问题,应用动力显式算法计算较合适。模拟在Abaqus软件中进行,弯曲角按表2进行。塑性变形要考虑加工硬化的影响,因此,采用加工硬化的塑性数据表征硬化方程:σp=K(ε0+ε)n。式中:k为材料系数;ε0为初始应变;ε为应变;n为硬化指数。摩擦模型采用从静态摩擦系数到动态摩擦系数的指定衰减模型,数学表达式为:
式中:动摩擦系数μk=0.2;静摩擦系数μs=0.3;衰减系数dc=1.5;γeq为滑移率。采用细网格划分的线性减缩积分单元。轧辊和板料的接触采用面-面模型。为缩短计算时间,在模拟中将板料成形速度设置(10m/s)大于实际。
4.2模拟结果与分析
图4、5分别为第1道次板料咬入过程图和第2道次强迫成形图,箭头为板材的运动方向。图6曲线A为图4位置的等效应力分布。可以看出,第1道次咬入过程中,板带前端与滚轮相接触的部分受力很大,未接触部分由前向后受力逐渐减小。由于前端受孔型作用发生弯曲,带动板料两侧逐渐弯曲变形。当自由端运动到第2道次滚轮时,由于受第1道次推动和第2道次滚轮对型材的摩擦力,自由端被逐渐咬入第2道次孔型中。曲线B为图5的等效应力分布。可以看出,自由成形区前端受力较大,由前向后受力逐渐减小。这是由于后一道次孔型弯曲角比前一道次大,前一道次孔型主要起约束作用,后一道次孔型主要对型材施加力使其再次发生弯曲。另外,辊的前端受力大小和区域均达到最大值,型材被抛出后,受力又逐渐减小。所以板材经过第2道次时的应力整体上明显大于经过第1道次时的应力。其它道次板材应力变化趋势和曲线B类似,但应力会随着弯曲角度的增加而逐渐增大。
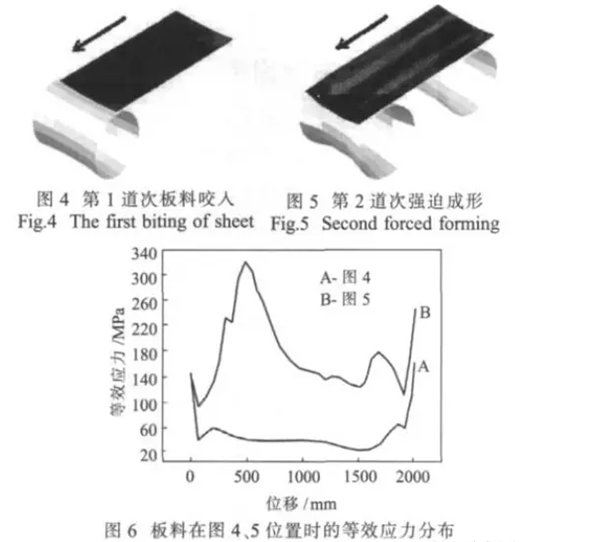
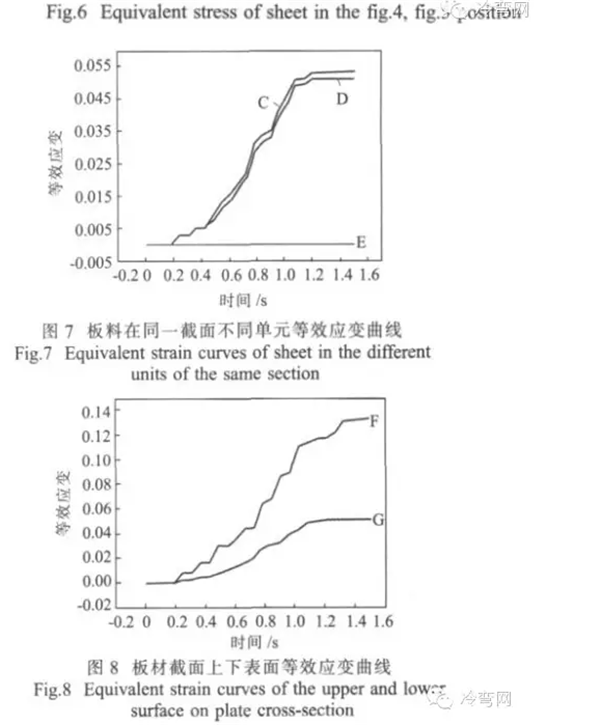
图7为板材在同一截面上不同单元随时间变化的等效应变曲线图。曲线C、D为板材弯角处的等效应变,曲线E为板材中部某单元的等效应变。可知,板材两边弯角处应变随时间不断增加。曲线E说明板材中部未产生塑性应变或应变很小。图8为板材在弯角处同一单元表面宽度方向随时间变化的等效应变曲线图。由图可知,上下表面的应变均随着时间的变化而不断增大,下表面(曲线F)的应变比上表面(曲线G)要大,且应变增速也大于上表面。
5 结语
研究发现,现有经验公式均有一定的使用范围,一些公式求解结果的误差很大;利用COPRA软件可以得到对时间具有参考价值的结果,使用时可结合经验公式以提高分析效率。数值模拟功能强大,所得信息完备,但对操作的要求较高,且分析计算效率较低。
| 下一条:电缆桥架行业仍然是全球和我国持续发展的新材料产业 | 上一条:简单生活轻钢别墅,为什么优势这么大? |















 联系方式
联系方式  产品类别
产品类别

 阿里巴巴
阿里巴巴